Computational engine: Syntax x = sparse_call(i, j, s, b); uses vectors i, j and s to generate a square full-rank sparse matrix A such that A(i(k),j(k)) = s(k), and solves the system of linear equations Ax=b. A must not be larger than ~50,000 x 50,000 for solution to converge. Download sparse_call (for 64-bit Windows, Matlab) sparse_call (for 64-bit Linux, Matlab) sparse_call (for 64-bit Linux, GNU Octave)

Description The main computational engine of the FEM Toolbox provides solution of the system of linear equations Ax=b, where A is large, sparse, and symmetric positive-definite matrix. We use iterative methods to solve the system of equations, and sparse matrix format to store and manipulate matrix A. Computational library for sparse matrices was written in C++ using templated classes and functions. It works under Linux and Windows. To demonstrate its capabilities, it has been used to create mex-function sparse_call(). Examples Here is an example demonstrating how to solve Ax=b, where sparse matrix A has different structures and different condition numbers. The quality of the solutions obtained with the sparse matrix library is compared with the Matlab solution using backslash operator x=A\b. In all cases the error is close to Matlab floating-point relative accuracy. Download test data (in rcv*.txt A is stored as coordinate list, and b*.txt stores vector b):  test data (11.18 MB) A=load('rcv1.txt'); b=load('b1.txt'); x=sparse_call(A(:,1)-1,A(:,2)-1,A(:,3),b); % compute Matlab solution using backslash: B=sparse(A(:,1),A(:,2),A(:,3)); x1=B\b; % generate figures: figure(11); spy(B) figure(12); plot(1:length(x1),x1,'ko'); axis square figure(13); plot(1:length(x),x-x1,'ko'); axis square In a similar way, one can obtain solutions for the other three examples using rcv2.txt with b2.txt, rcv3.txt with b3.txt, and rcv13.txt with b13.txt. Figures 1-4 illustrate results obtained from the test data.           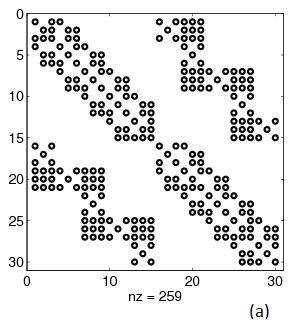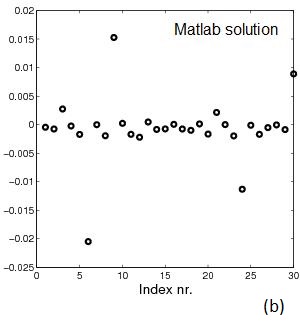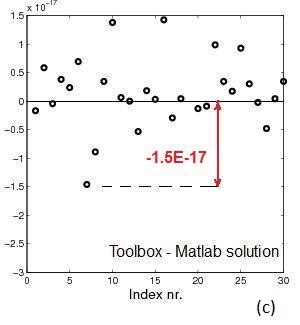Fig.1   Example 1. A is 30x30. 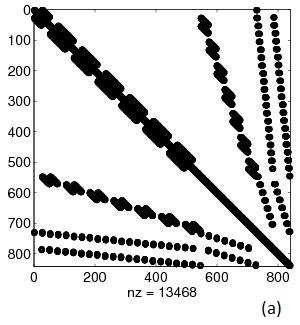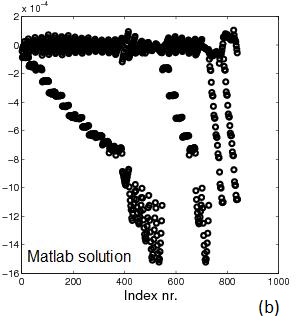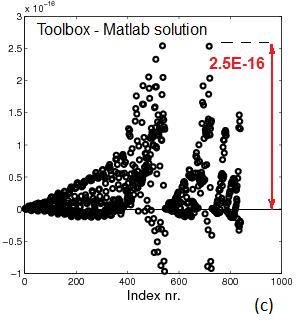cond(A)=3,175: (a) sparsity pattern of A, (b) Matlab solution x=A\b, (c) error between solution using Matlab's "\" and sparse_call()           Fig.2   Example 2. A is 840x840. 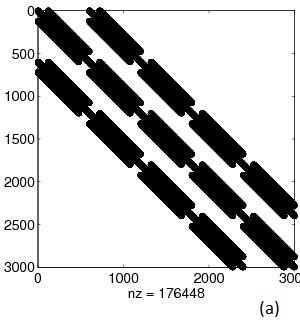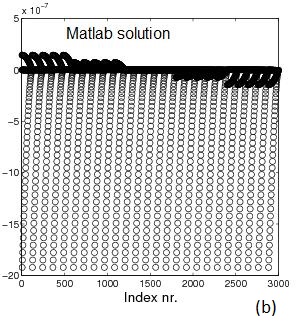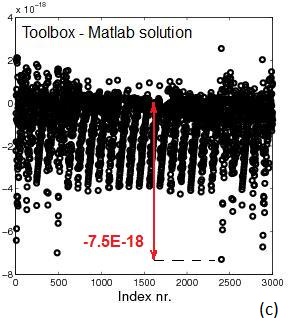cond(A)=695,088: (a) sparsity pattern of A, (b) Matlab solution x=A\b, (c) error between solution using Matlab's "\" and sparse_call()           Fig.3   Example 3. A is 3,000x3,000. 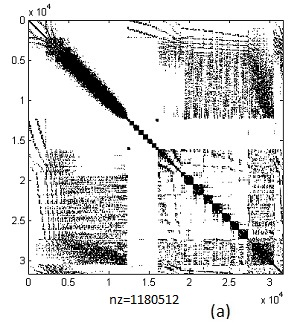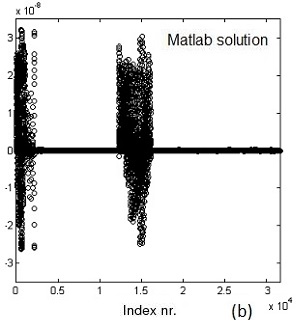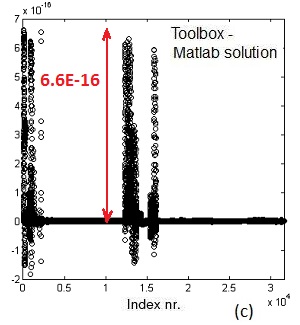cond(A)=2,993,749: (a) sparsity pattern of A, (b) Matlab solution x=A\b, (c) error between solution using Matlab's "\" and sparse_call()           Fig.4   Example 4. A is 31,581x31,581. cond(A)=708,400: (a) sparsity pattern of A, (b) Matlab solution x=A\b, (c) error between solution using Matlab's "\" and sparse_call()